霍夫变换（Hough Transform）

简介

霍夫变换（Hough Transform）最初用于检测图像中的直线或者圆等几何图形，主要应用在图像分析、计算机视觉和数字图像处理领域。后来经过拓展，可适用于任意图形的检测，及一些参数取值的检测。

霍夫直线变换的基本思想

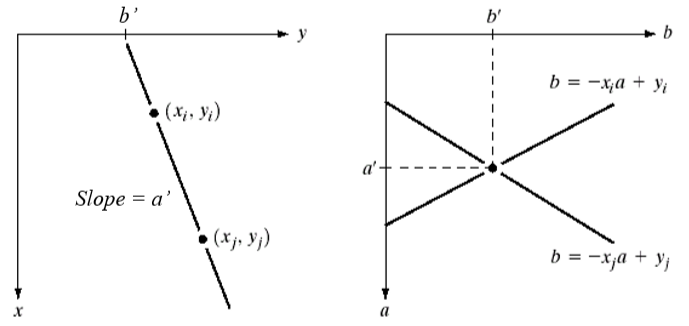
如果两点 (x_i, y_i) 和 (x_j, y_j) 都在一条直线上，那么它们在x-y平面上有相同的斜率和y轴的截距。

对于一个点 (x_i, y_i) ，经过直线 y_i = ax_i + b，其中a为斜率，b为y轴截距。可以把该式改写为 b = (-x_i)a+ y_i ，使a为自变量，b为因变量，a可取[a_min, a_max]，代入a可求出对应的b值。a和b的关系可以在参数空间（即a-b平面）上作图。把参数空间分隔为一个一个格子（累加器），然后把 (a, b) 对应的格子A(a, b) 加 1。
也就是说，一个点可以使参数空间的一系列累加器都加 1。

对于另外一个点 (x_j, y_j) ，把 y_j = ax_j + b 改写为 b = (-x_j)a+ y_j ，作同样的操作，对应的一系列累加器加1。

然后把所有点都如法炮制。在参数空间中，必然有一些累加器的值是比较大的，这些累加器对应的 (a, b) 值便是原图中可能的直线的参数。

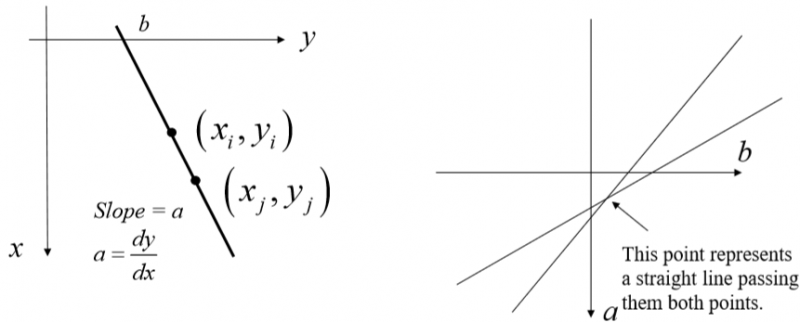
这样，即实现了把原始图像中给定直线的检测问题，转化为寻找参数空间的(局部)最大值问题。
然而，以上方法存在一个缺陷：若斜率不存在或无穷大，将导致a, b 的值也无穷大，需要无限个累加器，而这是不可能的。

因此，后来又提出了直线的另外一种表示方法：ρ = xcosθ + ysinθ，其中ρ是原点到直线上最近点的距离，θ是x轴与连接原点和最近点直线之间的夹角，如下图所示。

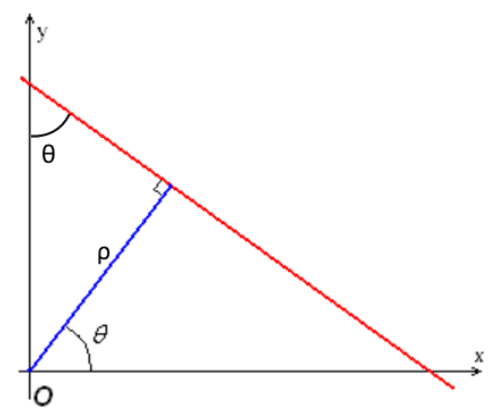
ρ = xcosθ + ysinθ 可由一开始的 y = ax + b 推得。斜率 a 等于 -cotθ，y 轴截距 b 等于 ρ/sinθ，即 y = -cotθ · x + ρ/sinθ。

因此，图像中的每一条直线可与一对参数 (ρ, θ) 相关联。这个参数(ρ, θ) 平面有时被称为霍夫空间，用于二维直线的集合。

由辅助角公式 asinx + bcosx = √(a²+b²)sin(x+arctan(b/a)) 可知，给定x和y的值，ρ = xcosθ + ysinθ 的图像将是一条正弦曲线。其中 -90°≤θ≤90°，-√2 D≤ρ≤√2 D，D为原图像的对角线长度。这样累加器的数目就可以控制，例如 θ 精确到 1°，ρ 取整。

所以我们可以得到一个结论，给定平面中的单个点，那么通过该点的所有直线的集合对应于 (ρ, θ) 平面中的一条正弦曲线。

例子

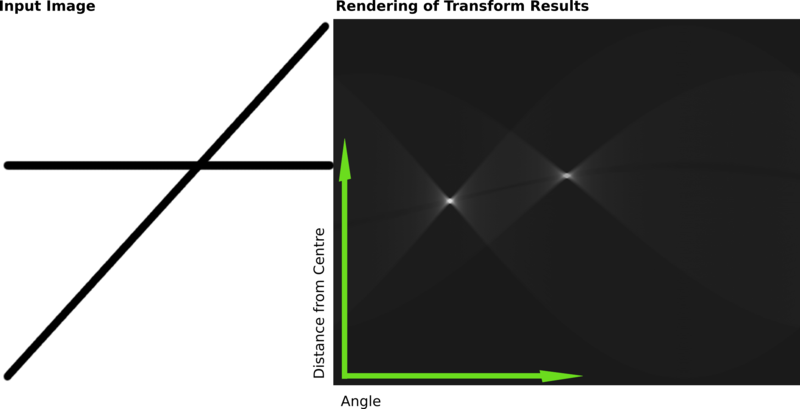
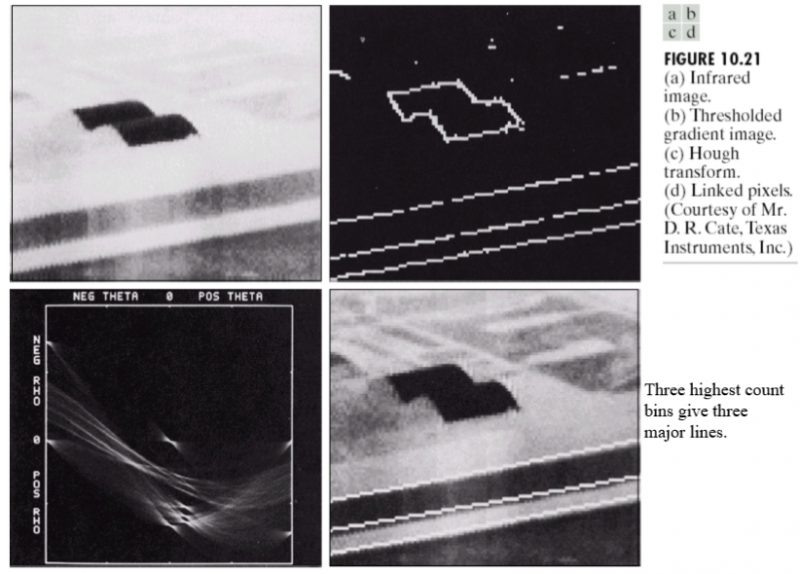
下图是包含两条粗线的光栅图像上的霍夫变换结果的例子。右下图中，越亮的地方代表累加器越大的值，可以从中看出原图有2根直线。

对于下图中复杂一点的例子，其霍夫空间也会更复杂。可见值最高的3个累加器正确地找到了3条直线。

算法的实现

1. 读取原始图并转换成灰度图，采用边缘检测算子（如Canny）转换成二值化边缘图像；
2. 对该图像进行霍夫变换；
3. 找到大于阈值的累加器，和对应的 ρ, θ 参数。

概率霍夫变换

用刚才的方法，找到的都是直线；而我们在实际应用中，可能更关心线段的提取。这就需要概率霍夫变换（Probabilistic Hough Transform）。

概率霍夫变换在 skimage、openCV 等库中均有实现，就不从底层开始推导了。它需要 minLineLength（线段的最短长度）和 maxLineGap（线段间允许的最大间隔，间隔之内的2条线段将被连接成1条线段）等参数。代码可参考文末的 openCV 文档。

例子

霍夫圆变换

类似的，要在原图中定位圆，给定平面中的一个点且半径已知，则通过该点的所有圆的集合对应于一个圆，类似“3点确定一个圆”的原理。

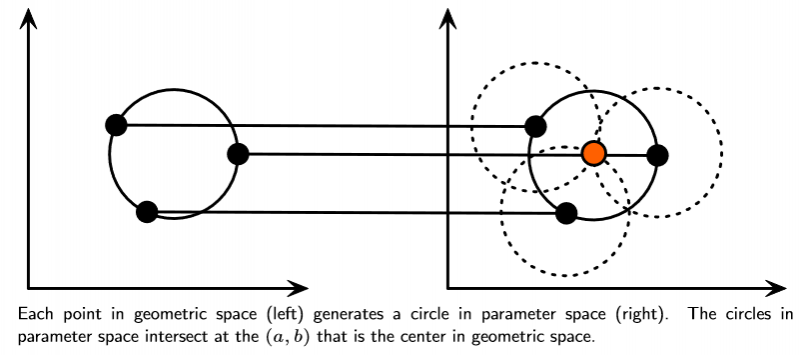
而当半径未知，则可在一定半径范围内进行搜索。当然，这会使性能下降。

算法的实现

1. 读取原始图并转换成灰度图，采用边缘检测算子（如Canny）转换成二值化边缘图像；
2. 给定半径R，对于每个图像中的边缘点(a, b)，按照参数方程 x = a + Rcos(θ) 和 y = b + Rsin(θ) 将那些可能是一个圆中心的单元格值进行累加；
3. 找到大于阈值的累加器，和对应的 a, b 参数；
4. 若半径未知，改变R的值，重复步骤2~3，直到遍历完半径范围。

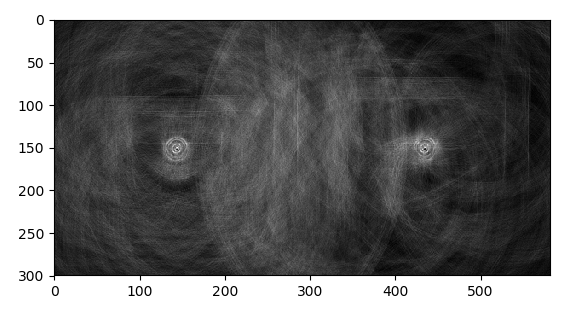
例子

相关参考

1. [Gonzalez and Woods] Rafael C. Gonzalez and Richard E. Woods, Chapter 10, Digital Image Processing, Second Edition, Pearson Education, Inc.
2. 经典霍夫变换（Hough Transform）, https://blog.csdn.net/yuyuntan/article/details/80141392
3. openCV doc, https://docs.opencv.org/3.4.5/d6/d10/tutorial_py_houghlines.html
4. Harvey Rhody, Hough transformfor detecting circles