Alpha-Beta剪枝用于裁剪搜索树中不需要搜索的树枝,以提高运算速度。它基本的原理是:
- 当一个 Min 节点的 β值≤任何一个父节点的α值时 ,剪掉该节点的所有子节点
- 当一个 Max 节点的 α值≥任何一个父节点的β值时 ,剪掉该节点的所有子节点
下面为只使用 MiniMax 和使用 Alpha-Beta 剪枝的简单对比。
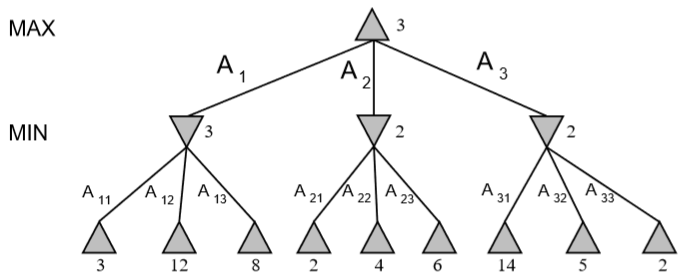
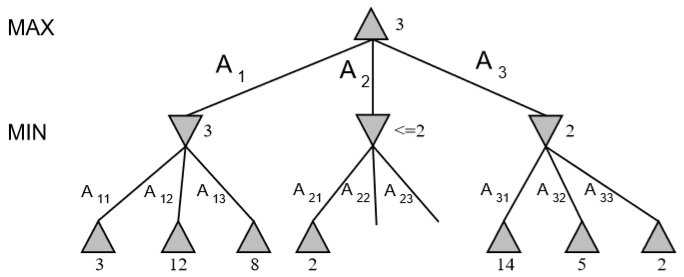
需要注意的是,剪枝的效果与树节点的访问顺序有关。
Alpha-Beta剪枝的伪代码如下:
Initialize MAX_VALUE(node,game,-∞,∞)
function MAX_VALUE(state,game,α,β) returns the minimax value of state
inputs: state, current state in game
game, game description
α, the best score for MAX along the path to state
β, the best score for MIN along the path to state
if CUTOFF_TEST(state) then return EVAL(state)
for each s in SUCCESSORS(state) do
α = MAX(α, MIN_VALUE(s,game,α,β))
if α ≥ β then return β
end
return α
function MIN_VALUE(state,game,α,β) returns the minimax value of state
if CUTOFF-TEST(state) then return EVAL(state)
for each s in SUCCESSORS(state) do
β = MIN(β, MAX_VALUE(s,game,α,β))
if α ≥ β then return α
end
return β下面用一个例子说明。规定从左节点开始展开。原搜索树为:
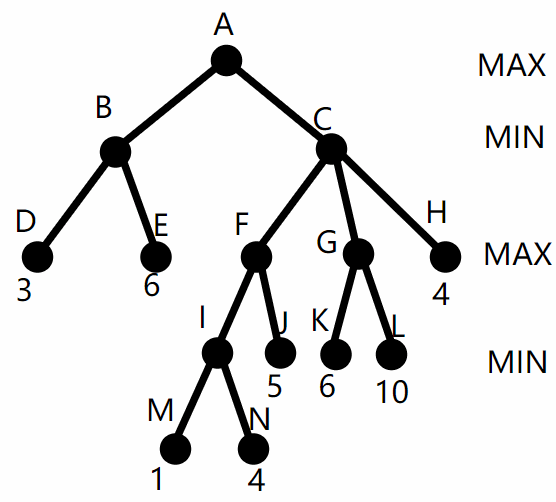
从根节点开始,初始化根节点的 α=-∞,β=∞,向左边的子节点展开。到D节点时,得到D的值为3,返回B节点,由于B节点是Min节点,所以更新B节点的β值为min(∞, 3)=3,如下图:
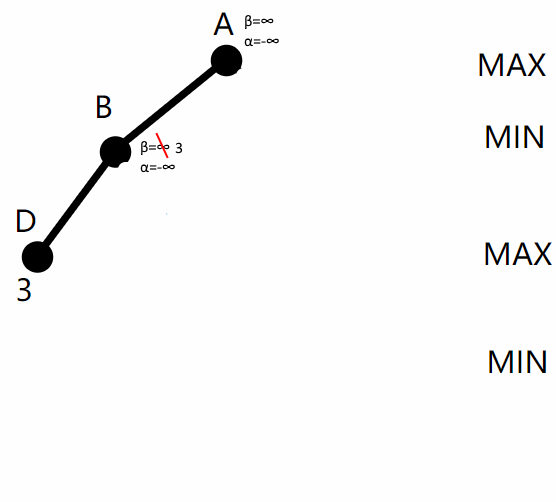
接下来从B到E,再从E返回B,min(3,6)仍为3。从B返回根节点A,A是 Max 节点,更新A的α值为 max(-∞, 3[B的β值])=3,如下图:
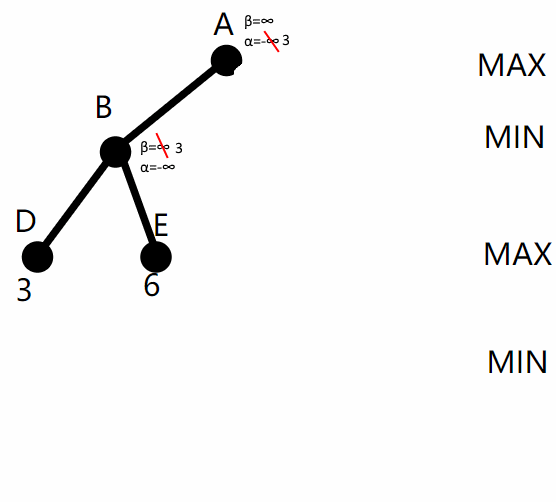
接下来从根节点往右深入,把根节点的 β=∞, α=3 依次传给C、F、I,从 I 深入 M再返回时,I 是 Min 节点,更新 I 的 β = min(∞, 1) = 1。留意到此时 I 的 α=3 > β,所以无需再探索 I 的剩余子节点,把未探索的子节点剪掉,如图3:
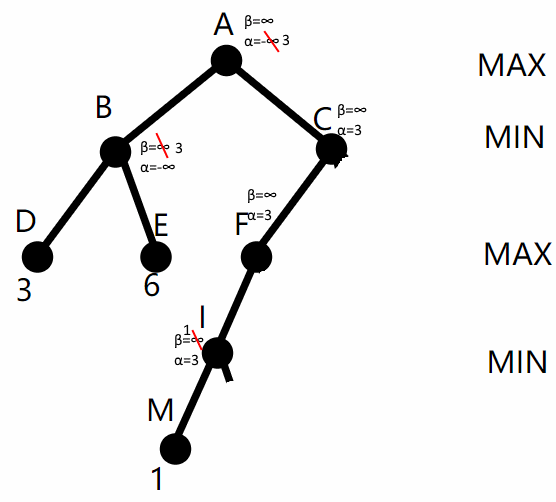
从节点 I 返回到F,F 的 α 值仍为 max(3, 1)=3不变。从F到J再返回,更新 F 的 α = max(3, 5) = 5。从 F 返回 C,更新 C 的 β = min(∞, 5) = 5,如图4:
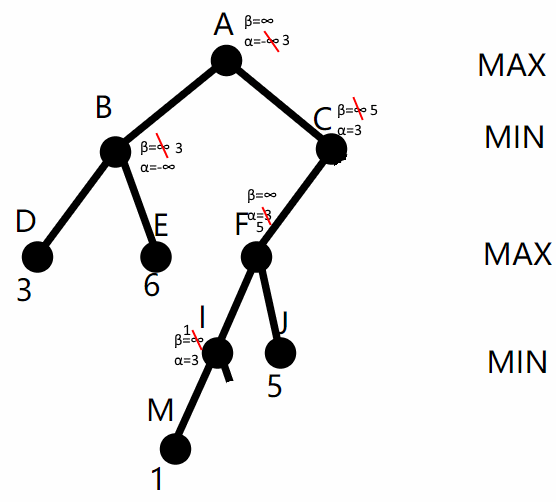
从 C 到 G,把 C 的 β=5, α=3 传给 G,从 G 到 K 再返回 G,更新 G 的 α = max(3, 6) = 6。注意到 G 的 α=6 >β,把 G 的其余子节点剪掉,如图5:
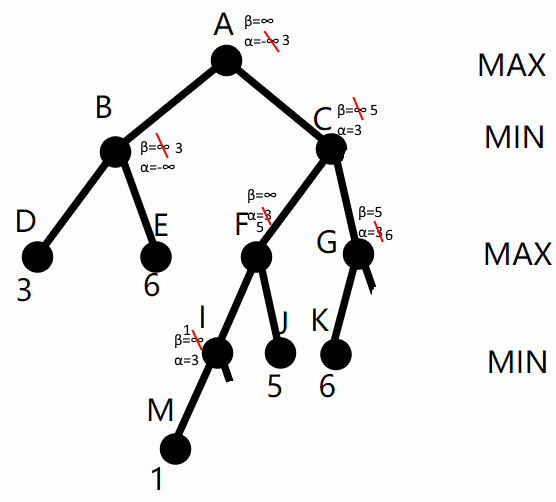
从 G 返回 C,C 的 β = min(5, 6) = 5 不变。从 C 到 H 然后返回,C 的 β = min(5, 4) = 4。
最后,从 C 返回根节点 A,A 是 Max 节点,A 的 α = max(3, 4[C的β值]) = 4,如图6:
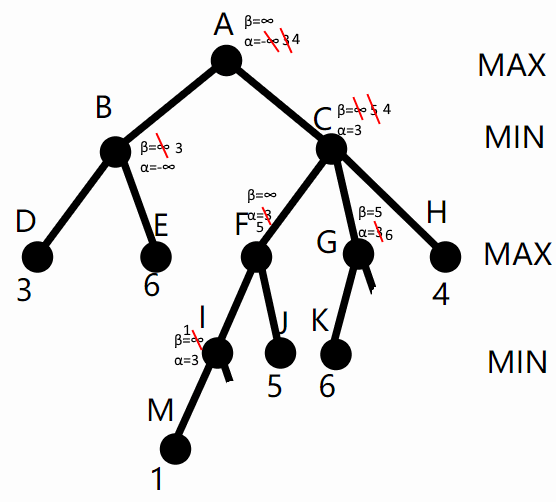
因此,在这个从左到右的 alpha-beta 剪枝中,节点 N 和 L 被剪掉了。
Question: 如果是从右到左,又会是哪些节点被裁剪呢?
相关参考
1. http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html
2. https://blog.csdn.net/tangchenyi/article/details/22925957
谢谢博主,看懂了
👍👍
一大堆人写这个,这篇是唯一一篇可以看懂的
这个真的超级绕啊,到底是什么样的人想出来的
大概这就是computer science吧😀
太好了,很清晰
多谢~~
感动,我居然看了一遍就学会了
很清晰,感谢!!一遍就看懂了
终于找到了一个讲解全过程的到了。感谢
其实这个是我之前做的一道题目,顺便分享一下😀
感谢大佬,终于看懂了,感谢!
泪目了
很清晰,谢谢作者!
Good,很清晰
感谢
作者,你是我滴神
呃,过奖了
比csdn上的大多数文章清晰orz
不能和csdn的比。。。😂