树状数组是一个能高效处理数组①更新、②求前缀和的数据结构。它提供了2 个方法,时间复杂度均为O(log n):
- update(index, delta):将 delta 加到数组的 index 位置
- prefix_sum(n):获取数组的前 n 个元素的和
range_sum(start, end):获取数组从 [start, end] 的和,相当于 prefix_sum(end) – prefix_sum(start-1)
如果只追求第 1 点,即快速修改数组,普通的线性数组可满足需求。但对于 range sum(),需要O(n)。
如果只追求第 2 点,即快速求 range sum,使用前缀数组的效果更好。但对于 add() 操作,则需要O(n),所以只适合更新较少的情况。
树状数组则处于两者之间,适合数组又修改,又获取区间和的情景。
思想
树状数组的思想是怎样的呢?
假设有一个数组 [1, 7, 3, 0, 5, 8, 3, 2, 6, 2, 1, 1, 4, 5],想求前 13 个元素的和。那么,
13 = 23 + 22 + 20 = 8 + 4 + 1
前 13 个数的和等于【前 8 个数的和】+【接下来 4 个数的和】+【接下来 1 个数的和】,即 range(1, 13) = range(1, 8) + range(9, 12) + range(13, 13)。如果有一种方法,可以保存 range(1, 8)、range(9, 12)、range(13, 13),那么计算这个区间和就可以加快了。
这里给出已经计算好的结果(即最下面的 array 层)。例如 array[8] 是 29,往上可以找到 29 对应的是 [1,8],即 range(1, 8) = array[8]。同理,range(9, 12) = array[12],range(13, 13) = array[13]。
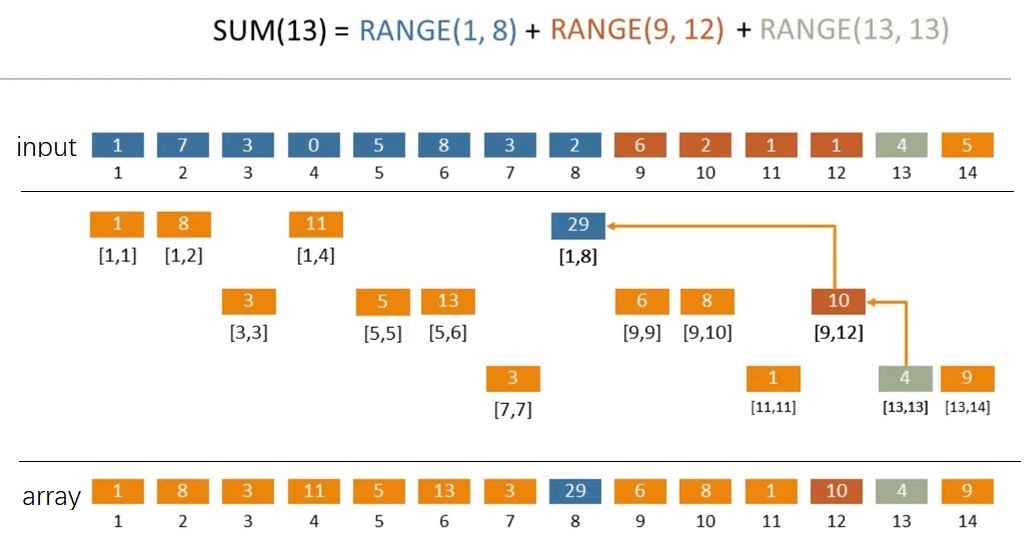
由此图可以发现,虽然它的英文是含有 Tree,中间的部分看起来也是树状的,但是最终用到的 array 是线性的数组(太好了,复杂程度大减)。
那中间这 3 层是怎么来的呢?——需要从上到下,从左到右看。
首先计算 [1, 1] 的和,然后计算 [1, 2] 的和,然后计算 [1, 4]、[1, 8] 的和,每次乘 2,直到越界([1, 16] 越界),这里分别算出来了1、8、11、29。
然后是第二层,从空缺的位置继续,这里的“界”不是整个数组的最大值,而是所有上层中下一个非空缺的位置。计算 [3, 3] 的和,[3, 4] 不用算,因为越界了。然后计算 [5, 5] 的和,接下来是 [5, 6] 的和,[5, 8] 越界不用算。
第三层也是类似,然后发现填完了。
以上可以帮助理解 result 数组中各值的来源,实际建立时有更简洁的做法。至于为什么是这样定义,可以另外找找资料,我看起来这有点像“分形”的感觉。
前缀和
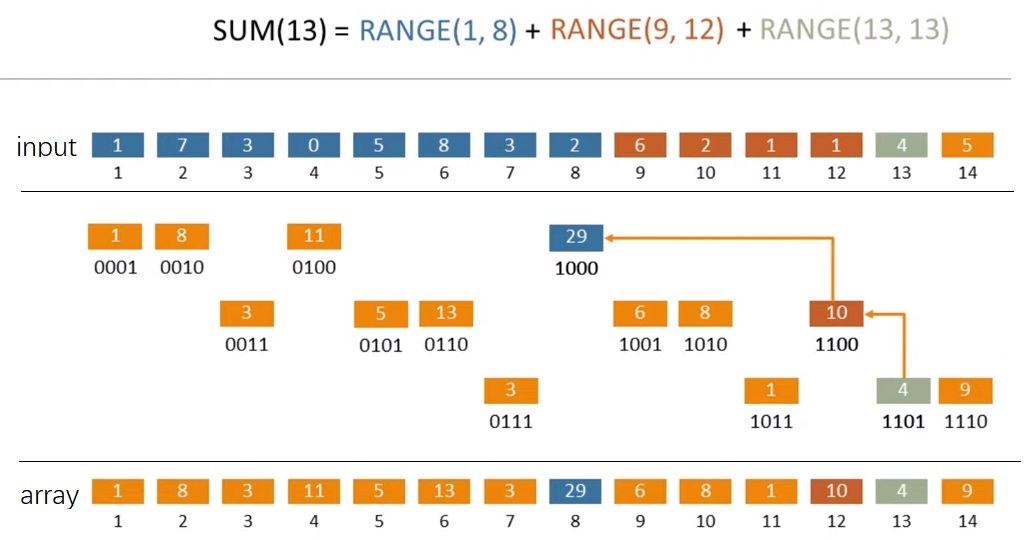
回到刚才的等式:range(1, 13) = range(1, 8) + range(9, 12) + range(13, 13) = array[8] + array[12] + array[13],这个 13 还好说,12 和 8 是怎么来的呢?
当然我们可以回到之前的 13 = 8 + 4 + 1,8 就是 8,12 就是 8+4,13 就是 8+4+1。先从 13 开始,然后减 1 得 12,接着减 4 得 8。树状数组的发明者利用 LSB(Least Significant Bit) 来实现:
range_sum(1, 13) = prefix_sum(13) = prefix_sum(0b1101) = array[0b1101] + array[0b1100] + array[0b1000]
可以发现,13 的二进制是 0b1101,就先取 array[0b1101];
然后把 0b1101 最后的 1 减掉【即减1】,变成 0b1100,就加上 array[0b1100];
接下来把 0b1100 最后的 1 减掉【即减4】,变成 0b1000,加上array[0b1000]。
这听起来有点复杂,但是计算机计算位运算是很简单的:LSB(x) = x & (-x),即可获取最后一个“1”对应的值。
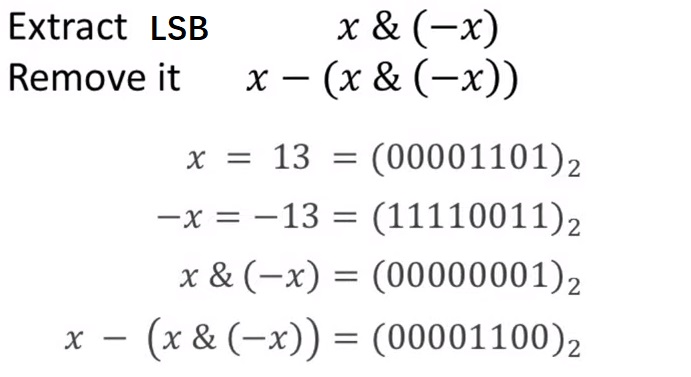
还是以 13 为例子,令 x=13,计算 x – LSB(x) 即可得到 12;再次计算即可得 8;再计算得 0,得到 0 就知道可以结束了。
讲了这么多,实现起来却很简单:给定长度为 n+1 的已经处理好的 array,计算 prefix_sum 的代码如下,核心函数 _prefix_sum() 只有 6 行:
def _lsb(n: int) -> int:
return n & (-n)
def _prefix_sum(array: list, index: int):
index += 1 # 算法内部,数组从1而不是0开始
result = 0
while index != 0:
result += array[index]
index -= _lsb(index)
return result
def range_sum(array: list, start: int, end: int):
""" 计算数组 [start, end] 闭区间的和 """
return _prefix_sum(array, end) - _prefix_sum(array, start - 1)
更新
现在考虑更新操作:将增量 delta 加到数组的 index 位置。
例如,想给第 5 个元素增加 2。显然,array[5] 需要增加 2,然后找一下有哪些 range 是包括第 5 个元素的——找到了 array[6](区间 [5, 6])、array[8](区间 [1, 8])。5、6、8 之间又有怎样的关系呢?
5 = 0b0101 6 = 0b0110 8 = 0b1000
发现 6 = 5 + LSB(5),8 = 6 + LSB(8)。这也太神奇了🤪。
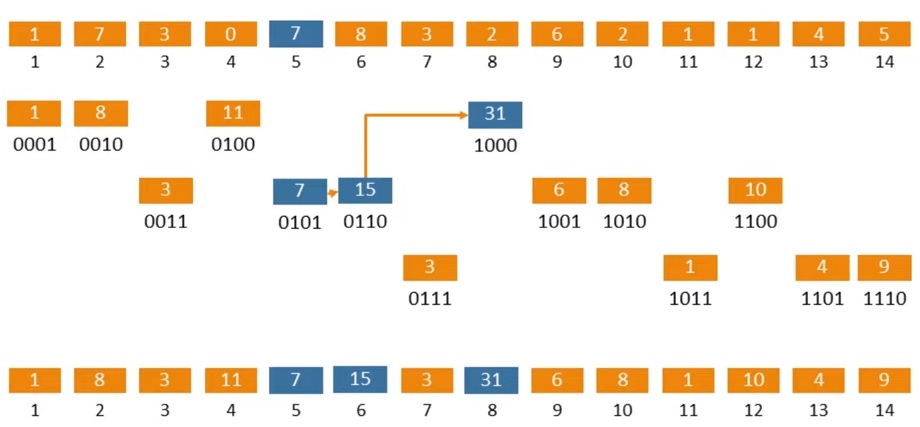
所以更新的实现也很简单:
def update(array: list, index: int, delta):
index += 1
while index < len(array):
array[index] += delta
index += _lsb(index)
建立
有了 update(),由已有的数组建立一个树状数组也是相当简单。首先初始化一个长度为 n+1 的全 0 数组,然后从 1~(n+1) 依次调用 update(),把已有数组的每一个元素加到全 0 数组中即可。这个过程的时间复杂度为O(n log n)。
另外有一个O(n)的建立方法,这里略过,可参考文末的链接。
Python 实现
import random
class BinaryIndexedTree:
def __init__(self, init_list: list):
self._array = [0] * (len(init_list) + 1)
for i, value in enumerate(init_list):
self.update(i, value)
def __len__(self):
""" 内部处理时长度加一,减一后对外部的长度才不变 """
return len(self._array) - 1
@staticmethod
def _lsb(n: int) -> int:
return n & (-n)
def _prefix_sum(self, index: int):
index += 1
result = 0
while index != 0:
result += self._array[index]
index -= self._lsb(index)
return result
def range_sum(self, start: int, end: int):
""" 计算数组 [start, end] 闭区间的和 """
return self._prefix_sum(end) - self._prefix_sum(start - 1)
def update(self, index: int, delta):
index += 1
while index < len(self._array):
self._array[index] += delta
index += self._lsb(index)
if __name__ == "__main__":
MAX = 10000
LENGTH = 1000
test_data = [random.randint(1, MAX) for _ in range(LENGTH)]
binary_indexed_tree = BinaryIndexedTree(test_data)
print(f'the sum of [12, 345] is {sum(test_data[12:346])} (by simple addition)')
print(f'the sum of [12, 345] is {binary_indexed_tree.range_sum(12, 345)} (by binary indexed tree)')
# 随便找10个元素,各加上随机值
for _ in range(10):
random_index = random.randint(0, LENGTH-1)
random_delta = random.randint(1, MAX)
test_data[random_index] += random_delta
binary_indexed_tree.update(random_index, random_delta)
print('\nafter updating some data')
print(f'the sum of [123, 666] is {sum(test_data[123:667])} (by simple addition)')
print(f'the sum of [123, 666] is {binary_indexed_tree.range_sum(123, 666)} (by binary indexed tree)')
Kotlin 实现
import kotlin.random.Random
import kotlin.random.nextInt
class BinaryIndexedTree(list: List<Int>) {
private val array = MutableList(list.size + 1) { 0 }
init {
for ((i, value) in list.withIndex())
update(i, value)
}
private fun lsb(n: Int) = n and (-n) // bitwise and
private fun prefixSum(index: Int): Int {
var index = index + 1
var result = 0
while (index != 0) {
result += this.array[index]
index -= lsb(index)
}
return result
}
fun rangeSum(start: Int, end: Int) = prefixSum(end) - prefixSum(start - 1)
fun update(index: Int, delta: Int) {
var index = index + 1
while (index < this.array.size) {
this.array[index] += delta
index += lsb(index)
}
}
}
fun main() {
val MAX = 10000
val LENGTH = 1000
val testData = MutableList(LENGTH) { Random.nextInt(1..MAX) }
val binaryIndexedTree = BinaryIndexedTree(testData)
println("the sum of [12, 345] is ${testData.subList(12, 346).reduce { a, b -> a + b }} (by simple addition)")
println("the sum of [12, 345] is ${binaryIndexedTree.rangeSum(12, 345)} (by binary indexed tree)")
// 随便找10个元素,各加上随机值
for (i in 1..10) {
val randomIndex = Random.nextInt(0 until LENGTH)
val randomDelta = Random.nextInt(1..MAX)
testData[randomIndex] += randomDelta
binaryIndexedTree.update(randomIndex, randomDelta)
}
println("\nafter updating some data")
println("the sum of [123, 666] is ${testData.subList(123, 667).reduce { a, b -> a + b }} (by simple addition)")
println("the sum of [123, 666] is ${binaryIndexedTree.rangeSum(123, 666)} (by binary indexed tree)")
}
发表评论