前言
首先,什么是反向代理?下图解释了它与正向代理的区别。
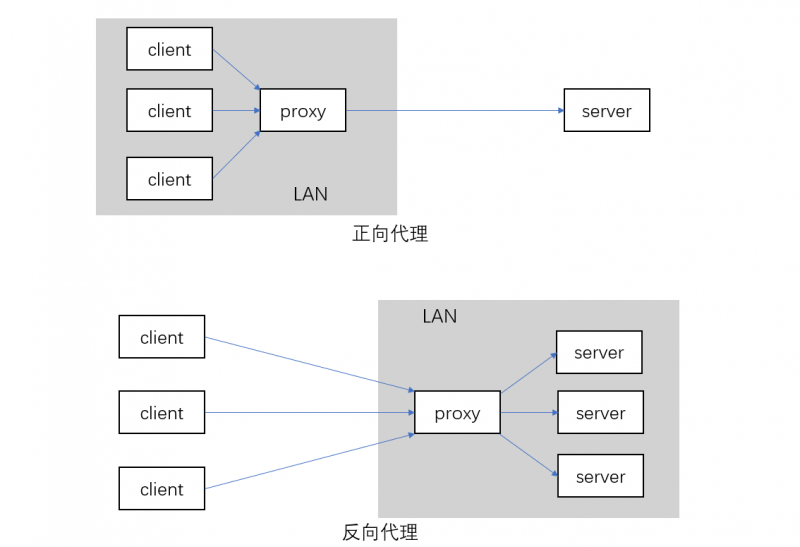
本质上,都是网络代理。正向代理更偏向于 client 端,而反向代理更偏向 server 端。(其实这个概念并不太重要)
阅读更多…Numba 是 Python 的一个 JIT (just-in-time) 编译器,最适用于 NumPy 数组、函数,以及 Python 循环。基本上,用法就是给原来的 Python 函数加一个修饰器,当运行到经 Numba 修饰的函数时,它会被编译为机器码,之后再调用时,就能以机器码的速度来执行了。
按我上手使用的经验来看,Numba 对原代码的改动不是太大,对能加速的部分,加速效果明显;对不支持的加速的 Python 语句/第三方库,可以选择不使用 numba 来规避。这是我选择 Numba 的原因。
由于 Numba 本身的限制(稍后介绍),不能做到对整个程序完全的优化。实际上,也没必要这样做——只需要优化真正耗时间的部分即可。
怎么找到真正耗时间的部分?除了靠直觉,还可以借用工具来分析,例如 Python 自带的 cProfile,还有 line_profiler 等,这里不再细讲。
可以通过 conda 或 pip,一个命令安装:
conda / pip install numba
按照官方文档的示例代码,如果代码中含有很多数学运算、使用 NumPy,或者有大量 Python 的 for 循环(这可是 Python 性能大忌),那么 Numba 就能给你很好的效果。尤其是多重 for 循环,可以获得极大的加速。
大家都知道,给一个 np.ndarray 加 1 是很快的(向量化、广播),但是如果 for 遍历这个 array 的元素再每个加 1就会很慢(新手容易犯的小错误);但是这都没关系,有了 Numba 再 for 遍历元素加 1,和直接用 ndarray 加 1 的耗时是差不多的!
再举个例子,下面这段代码,就能享受到 JIT:
from numba import jit
import numpy as np
x = np.arange(100).reshape(10, 10)
@jit(nopython=True) # 设置为"nopython"模式 有更好的性能
def go_fast(a): # 第一次调用时会编译
trace = 0
for i in range(a.shape[0]): # Numba likes loops
trace += np.tanh(a[i, i]) # Numba likes NumPy functions
return a + trace # Numba likes NumPy broadcasting
print(go_fast(x))但是,类似下面的代码,Numba 就没什么效果:
from numba import jit
import pandas as pd
x = {'a': [1, 2, 3], 'b': [20, 30, 40]}
@jit
def use_pandas(a): # 这个函数就加速不了
df = pd.DataFrame.from_dict(a) # Numba 不支持 pd.DataFrame
df += 1 # Numba 也不支持这个
return df.cov() # 和这个
print(use_pandas(x))总之,Numba 应付不了 pandas。以我的经验,需要先把 DataFrame 转成 np.ndarray,再输入给 Numba。
刚才有效果的代码中,@jit(nopython=True) 这里传入了 nopython 这个参数,而没什么效果的代码中,就没有这个参数。为什么呢?
这是因为,@jit 实际上有两种模式,分为别 nopython 和 object 模式。只有 nopython 模式,才是能真正大幅加速的模式。而 nopython 模式只支持部分的 Python 和 NumPy 函数,如果运行时用到了不支持的函数/方法,程序就会崩掉 (例如刚才不能加速的例子如果加上 nopython 就会崩) 。如果不强制设定 nopython 模式,编译函数失败时,会回退到 object 模式,程序虽然不会崩,但却偏离了我们给它加速的本意。
我既然用了 Numba,我就希望它能真正地发挥作用。所以选择强制开启 nopython ,如果不能加速,不如让它直接崩溃,我们再作对应修改。
阅读更多…相比A股和港股,(免费的)美股的数据没有那么容易拿到,而适合Python的source/library就更少了。
最近找到一个免费、轻量的Python库——yfinance。整个库只有几个文件,数据从yahoo下载,免费无限制。安装及使用教程见上面的链接。
无需申请token,即装即用,和tushare一样方便,值得拥有。赶紧 pip install 一个吧。
附上 github 上的一点使用文档:
import yfinance as yf
msft = yf.Ticker("MSFT")
# get stock info
msft.info
# get historical market data
hist = msft.history(period="max")
# show actions (dividends, splits)
msft.actions
# show dividends
msft.dividends
# show splits
msft.splits
# show financials
msft.financials
msft.quarterly_financials
经本文的评论指出,本文中的代码的原理可能有严重的问题。当作是学习 pytorch 的语法就好了,在修复之前不要用于学术用途。Don’t take it serious!能赚钱的算法都不会公开🤣
学习使用 LSTM 来预测时间序列,本文中使用上证指数的收盘价。
Python 3.5+, PyTorch 1.1.0, tushare
首先用 tushare 下载上证指数的K线数据,然后作标准化处理。
import numpy as np
import tushare as ts
data_close = ts.get_k_data('000001', start='2018-01-01', index=True)['close'].values # 获取上证指数从20180101开始的收盘价的np.ndarray
data_close = data_close.astype('float32') # 转换数据类型
# 将价格标准化到0~1
max_value = np.max(data_close)
min_value = np.min(data_close)
data_close = (data_close - min_value) / (max_value - min_value)
把K线数据进行分割,每 DAYS_FOR_TRAIN 个收盘价对应 1 个未来的收盘价。例如K线为 [1,2,3,4,5], DAYS_FOR_TRAIN=3,那么将会生成2组数据:
第1组的输入是 [1,2,3],对应输出 4;
第2组的输入是 [2,3,4],对应输出 5。
然后只使用前70%的数据用于训练,剩下的不用,用来与实际数据进行对比。
DAYS_FOR_TRAIN = 10
def create_dataset(data, days_for_train=5) -> (np.array, np.array):
"""
根据给定的序列data,生成数据集
数据集分为输入和输出,每一个输入的长度为days_for_train,每一个输出的长度为1。
也就是说用days_for_train天的数据,对应下一天的数据。
若给定序列的长度为d,将输出长度为(d-days_for_train+1)个输入/输出对
"""
dataset_x, dataset_y= [], []
for i in range(len(data)-days_for_train):
_x = data[i:(i+days_for_train)]
dataset_x.append(_x)
dataset_y.append(data[i+days_for_train])
return (np.array(dataset_x), np.array(dataset_y))
dataset_x, dataset_y = create_dataset(data_close, DAYS_FOR_TRAIN)
# 划分训练集和测试集,70%作为训练集
train_size = int(len(dataset_x) * 0.7)
train_x = dataset_x[:train_size]
train_y = dataset_y[:train_size]
# 将数据改变形状,RNN 读入的数据维度是 (seq_size, batch_size, feature_size)
train_x = train_x.reshape(-1, 1, DAYS_FOR_TRAIN)
train_y = train_y.reshape(-1, 1, 1)
# 转为pytorch的tensor对象
train_x = torch.from_numpy(train_x)
train_y = torch.from_numpy(train_y)
阅读更多… 大家都知道,Google有一个很方便的 Colab ,而且到目前为止,还是免费的,并且 GPU 和 TPU 也是免费的。那为什么还要自己搞呢?因为 Colab 每个 session 只能用12小时,之后环境和数据不会保留,并且也不能进一步自定义配置和性能。Google 云给新注册的用户提供了$300 USD的赠金,非常适合学生党和个人的小项目。下面就开始体验吧。
如果还没有 Google Cloud 用户,前往 Google Cloud 注册一个。这里需要一张 Visa / Mastercard 信用卡,没有的话我也帮不了你..然后$300 USD额度就到手了。
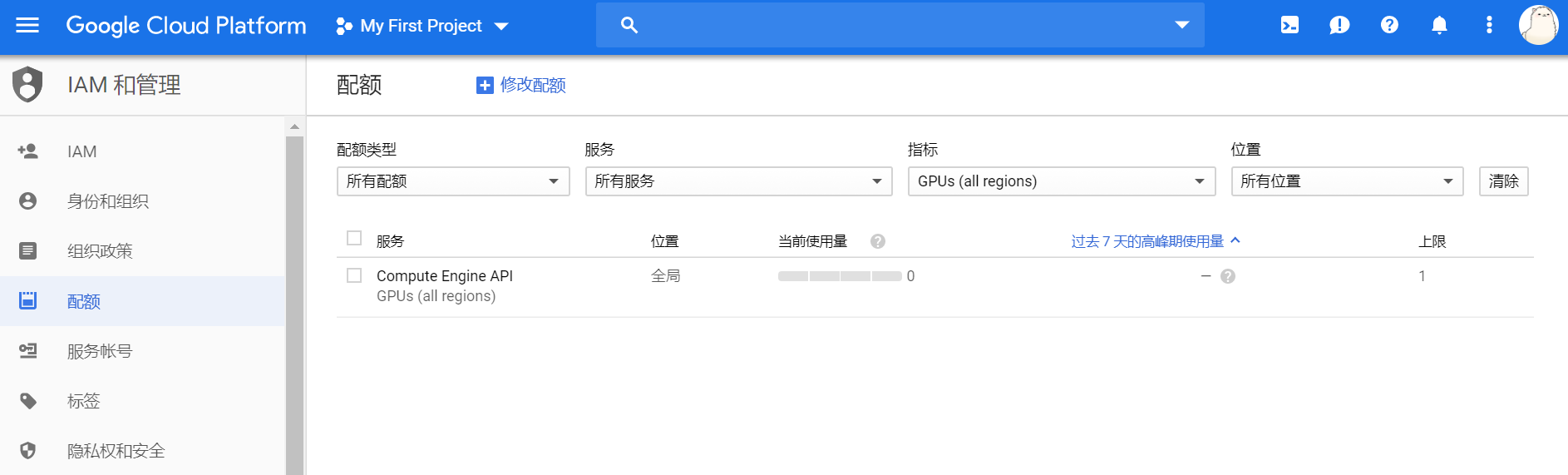
一开始的用户是没有 GPU 额度的,就算创建了带 GPU 的实例,也不能启动。请参照申请提升配额的步骤提交申请,把 GPU 的 0 改为更大的数值。在此之前,平台应该会让你把用户升级为付费账号,也就是说,如果送的额度用完了,就会从你的信用卡扣钱(注意要省着用了)。申请提升配额的页面中写可能要一两天来处理申请,但是我提交之后一小时内就批了。
Z3 是一个由 Microsoft Research 开发的定理求解器。它可以用在很多方面,如软/硬件的验证与测试、约束求解、混合系统的分析、安全、生物,以及求解几何等问题[1]。Z3 主要由 C++ 开发,但它支持被 .NET、C、C++、Java、Python 等语言调用。本文使用其 Python binding。
在网上看到有不少解方程和约束条件的使用,我在此补充它在命题逻辑方面的例子。
非Windows平台可尝试直接安装:
pip install z3-solver
Windows平台由于编译环境比较复杂,Pypi 中只有没这么新的版本,指定旧版本安装:
pip install z3-solver==4.5.1.0.post2
一军用仓库被窃,公安部门已掌握如下线索:①甲、乙、丙三人至少有一个是窃贼;②如甲是窃贼,则乙一定是同案犯;③盗窃发生时,乙正在影剧院看电影。由此可以推出( )。
A.甲、乙、丙都是窃贼
B.甲和乙都是窃贼
C.丙是窃贼
D.甲是窃贼
Alpha-Beta剪枝用于裁剪搜索树中不需要搜索的树枝,以提高运算速度。它基本的原理是:
下面为只使用 MiniMax 和使用 Alpha-Beta 剪枝的简单对比。
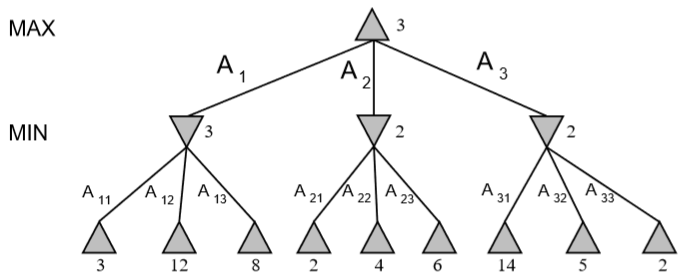
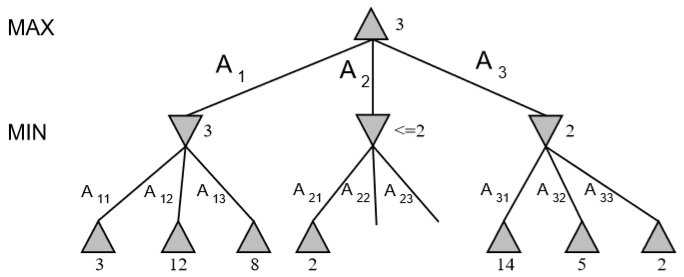
需要注意的是,剪枝的效果与树节点的访问顺序有关。
Alpha-Beta剪枝的伪代码如下:
Initialize MAX_VALUE(node,game,-∞,∞)
function MAX_VALUE(state,game,α,β) returns the minimax value of state
inputs: state, current state in game
game, game description
α, the best score for MAX along the path to state
β, the best score for MIN along the path to state
if CUTOFF_TEST(state) then return EVAL(state)
for each s in SUCCESSORS(state) do
α = MAX(α, MIN_VALUE(s,game,α,β))
if α ≥ β then return β
end
return α
function MIN_VALUE(state,game,α,β) returns the minimax value of state
if CUTOFF-TEST(state) then return EVAL(state)
for each s in SUCCESSORS(state) do
β = MIN(β, MAX_VALUE(s,game,α,β))
if α ≥ β then return α
end
return β下面用一个例子说明。规定从左节点开始展开。原搜索树为:
阅读更多…Harris算法和Shi-Tomasi 算法,由于算法原理,具有旋转不变性,在目标图片发生旋转时依然能够获得相同的角点。但是如果对图像进行缩放以后,再使用之前的算法就会检测不出来,如图:
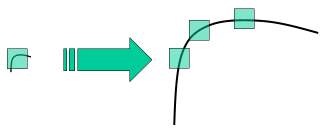
在2004年,University of British Columbia 的 D.Lowe 在他的论文 Distinctive Image Features from Scale-Invariant Keypoints 中提出了一个新的算法,Scale Invariant Feature Transform (简称SIFT),它可以提取关键点及计算其描述符。OpenCV的文档指出这篇论文容易理解,推荐阅读。
SIFT算法主要有4个步骤,详情请见文末的相关参考。
霍夫变换(Hough Transform)最初用于检测图像中的直线或者圆等几何图形,主要应用在图像分析、计算机视觉和数字图像处理领域。后来经过拓展,可适用于任意图形的检测,及一些参数取值的检测。
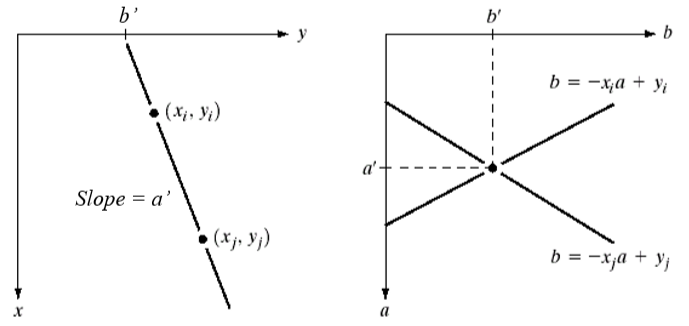
如果两点 (xi, yi) 和 (xj, yj) 都在一条直线上,那么它们在x-y平面上有相同的斜率和y轴的截距。
对于一个点 (xi, yi) ,经过直线 yi = axi + b,其中a为斜率,b为y轴截距。可以把该式改写为 b = (-xi)a+ yi ,使a为自变量,b为因变量,a可取[amin, amax],代入a可求出对应的b值。a和b的关系可以在参数空间(即a-b平面)上作图。把参数空间分隔为一个一个格子(累加器),然后把 (a, b) 对应的格子A(a, b) 加 1。
也就是说,一个点可以使参数空间的一系列累加器都加 1。
对于另外一个点 (xj, yj) ,把 yj = axj + b 改写为 b = (-xj)a+ yj ,作同样的操作,对应的一系列累加器加1。
阅读更多…