树状数组是一个能高效处理数组①更新、②求前缀和的数据结构。它提供了2 个方法,时间复杂度均为O(log n):
- update(index, delta):将 delta 加到数组的 index 位置
- prefix_sum(n):获取数组的前 n 个元素的和
range_sum(start, end):获取数组从 [start, end] 的和,相当于 prefix_sum(end) – prefix_sum(start-1)
如果只追求第 1 点,即快速修改数组,普通的线性数组可满足需求。但对于 range sum(),需要O(n)。
如果只追求第 2 点,即快速求 range sum,使用前缀数组的效果更好。但对于 add() 操作,则需要O(n),所以只适合更新较少的情况。
树状数组则处于两者之间,适合数组又修改,又获取区间和的情景。
思想
树状数组的思想是怎样的呢?
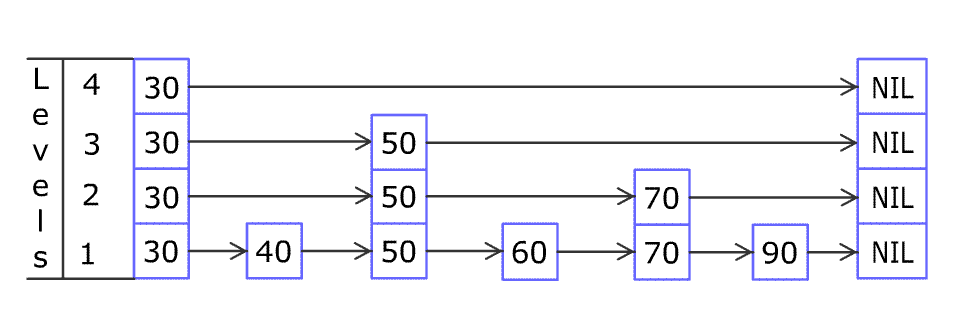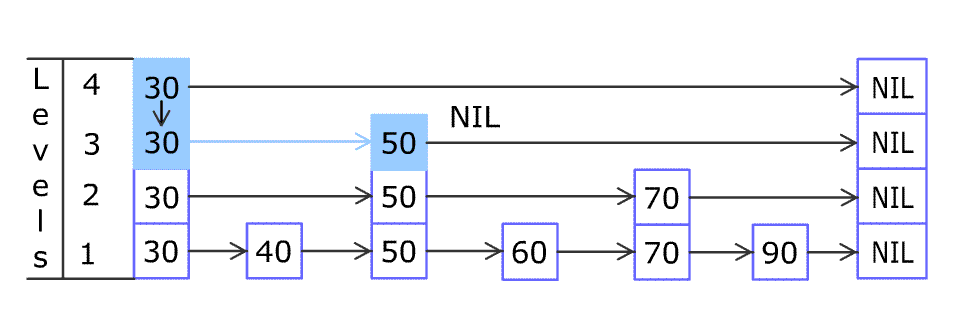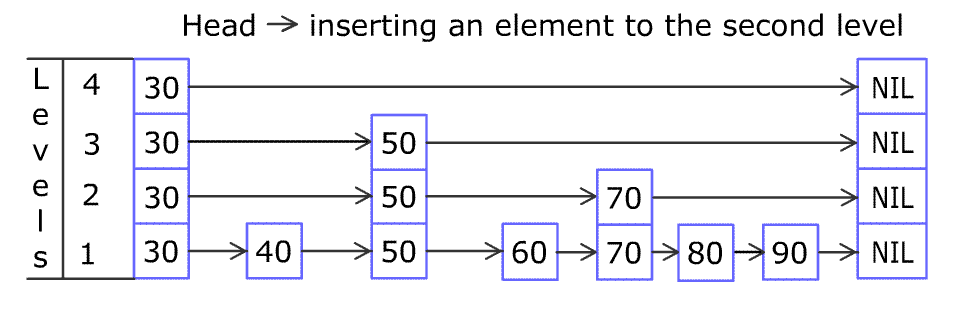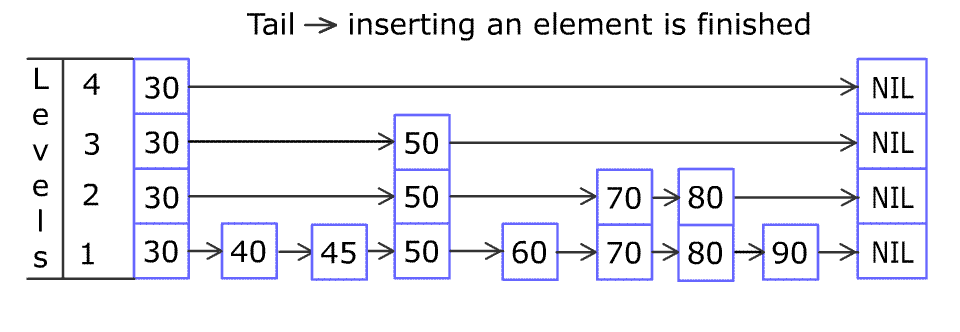
假设有一个数组 [1, 7, 3, 0, 5, 8, 3, 2, 6, 2, 1, 1, 4, 5],想求前 13 个元素的和。那么,
13 = 23 + 22 + 20 = 8 + 4 + 1
前 13 个数的和等于【前 8 个数的和】+【接下来 4 个数的和】+【接下来 1 个数的和】,即 range(1, 13) = range(1, 8) + range(9, 12) + range(13, 13)。如果有一种方法,可以保存 range(1, 8)、range(9, 12)、range(13, 13),那么计算这个区间和就可以加快了。
这里给出已经计算好的结果(即最下面的 array 层)。例如 array[8] 是 29,往上可以找到 29 对应的是 [1,8],即 range(1, 8) = array[8]。同理,range(9, 12) = array[12],range(13, 13) = array[13]。
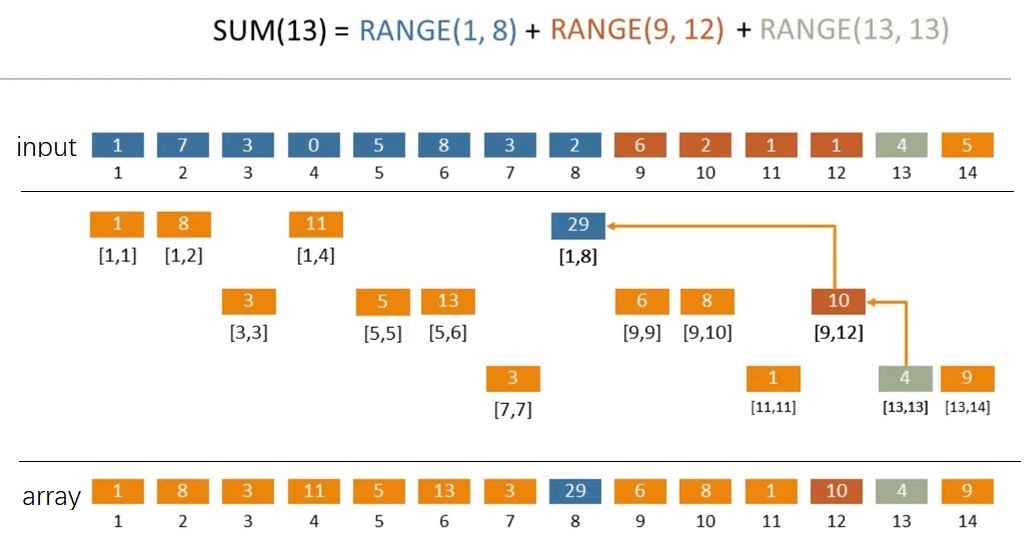
由此图可以发现,虽然它的英文是含有 Tree,中间的部分看起来也是树状的,但是最终用到的 array 是线性的数组(太好了,复杂程度大减)。
那中间这 3 层是怎么来的呢?——需要从上到下,从左到右看。
首先计算 [1, 1] 的和,然后计算 [1, 2] 的和,然后计算 [1, 4]、[1, 8] 的和,每次乘 2,直到越界([1, 16] 越界),这里分别算出来了1、8、11、29。
然后是第二层,从空缺的位置继续,这里的“界”不是整个数组的最大值,而是所有上层中下一个非空缺的位置。计算 [3, 3] 的和,[3, 4] 不用算,因为越界了。然后计算 [5, 5] 的和,接下来是 [5, 6] 的和,[5, 8] 越界不用算。
第三层也是类似,然后发现填完了。
以上可以帮助理解 result 数组中各值的来源,实际建立时有更简洁的做法。至于为什么是这样定义,可以另外找找资料,我看起来这有点像“分形”的感觉。
阅读更多…