• 使用 Python OpenCV 3.4.x 进行 SIFT 特征检测与匹配

    2018年12月24日 作者：7forz
    暂无评论

    前言

    Harris算法和Shi-Tomasi 算法，由于算法原理，具有旋转不变性，在目标图片发生旋转时依然能够获得相同的角点。但是如果对图像进行缩放以后，再使用之前的算法就会检测不出来，如图：

    图像放大，窗口不变，导致检测结果发生变化

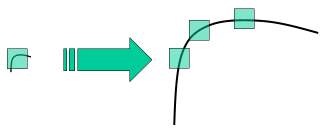
    在2004年，University of British Columbia 的 D.Lowe 在他的论文 Distinctive Image Features from Scale-Invariant Keypoints 中提出了一个新的算法，Scale Invariant Feature Transform (简称SIFT)，它可以提取关键点及计算其描述符。OpenCV的文档指出这篇论文容易理解，推荐阅读。

    SIFT算法主要有4个步骤，详情请见文末的相关参考。

    流程

    1. 尺度空间极值检测（Scale-space Extrema Detection）
    2. 关键点定位（Keypoint Localization）
    3. 方向分配（Orientation Assignment）
    4. 关键点描述符（Keypoint Descriptor）
    阅读更多…

  • 霍夫变换（Hough Transform）

    2018年12月23日 作者：7forz
    暂无评论

    简介

    霍夫变换（Hough Transform）最初用于检测图像中的直线或者圆等几何图形，主要应用在图像分析、计算机视觉和数字图像处理领域。后来经过拓展，可适用于任意图形的检测，及一些参数取值的检测。

    霍夫直线变换的基本思想

    如果两点 (xi, yi) 和 (xj, yj) 都在一条直线上，那么它们在x-y平面上有相同的斜率和y轴的截距。

    对于一个点 (xi, yi) ，经过直线 yi = axi + b，其中a为斜率，b为y轴截距。可以把该式改写为 b = (-xi)a+ yi ，使a为自变量，b为因变量，a可取[amin, amax]，代入a可求出对应的b值。a和b的关系可以在参数空间（即a-b平面）上作图。把参数空间分隔为一个一个格子（累加器），然后把 (a, b) 对应的格子A(a, b) 加 1。
    也就是说，一个点可以使参数空间的一系列累加器都加 1。

    对于另外一个点 (xj, yj) ，把 yj = axj + b 改写为 b = (-xj)a+ yj ，作同样的操作，对应的一系列累加器加1。

    阅读更多…