跳跃列表是一种随机数据结构。它使得包含 n 个元素的有序序列的查找、插入、删除操作的平均时间复杂度都是 O(log n)。(注意关键词有序,如果不需要有序,也不需要用到跳跃列表;数据量大时,时间复杂度退化到较慢的概率微乎其微)
| 平均 | 最差 | |
| 搜索 | O(log n) | O(n) |
| 插入 | O(log n) | O(n) |
| 删除 | O(log n) | O(n) |
| 空间 | O(n) | O(n log n) |
跳跃列表是通过维护一个多层的链表实现的。每一层链表中的元素的数量,在统计上来说都比下面一层链表元素的数量更少。也就是说,上层疏,下层密,底层数据是完整的,上面的稀疏层作为索引——这就是链表的“二分查找”啊。
一开始时,算法在最稀疏的层次进行搜索,直至需要查找的元素在该层两个相邻的元素中间。这时,算法将跳转到下一个层次,重复刚才的搜索,直到找到需要查找的元素为止。
Wikipedia 的道理就讲到这里,我不希望把本文写得难懂。说好的一图流就能领悟呢?其实我有点标题党,本文不止一幅图,但是核心的图只有一幅,上图(来自 Wikipedia):
请多次认真观看插入节点的全过程 gif。我看完之后,就觉得自己可以实现出来了(虽然后来实际开发调试了很多次)。
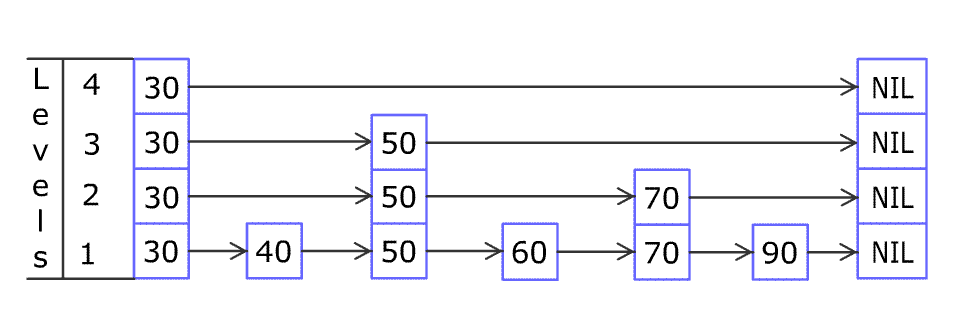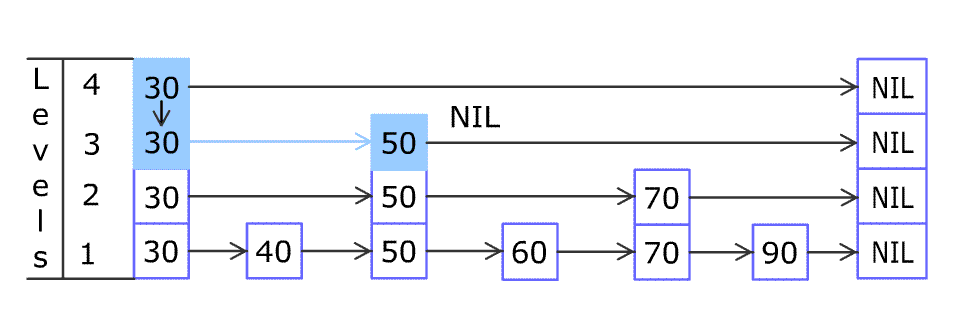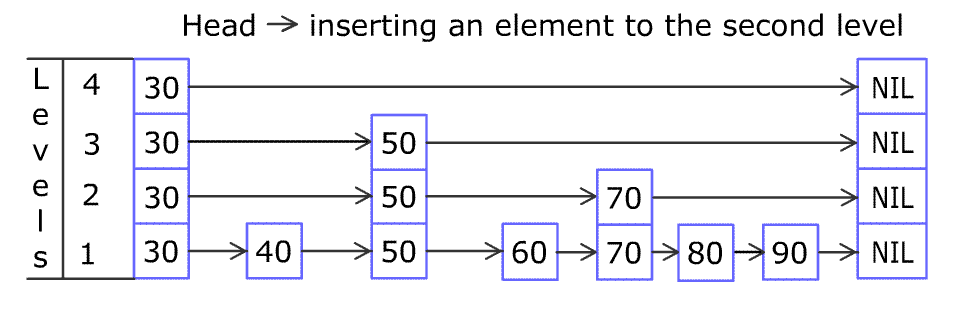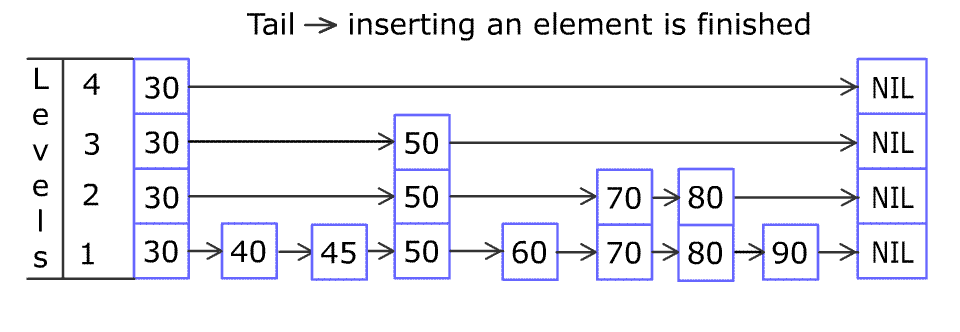
例如想在上图中所示的跳跃列表中插入 80,首先要找到应该插入的位置。
首先从最稀疏的层的 30 开始,把当前位置设置为顶层的 30。
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 30;
80 比当前位置右边的 50 大,所以把当前位置右移到 50;
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 50;
80 比当前位置右边的 70 大,所以把当前位置右移到 70;
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 70;(当前位置已到达底层)
之后用 80 不断与右边的节点比较大小,右移至合适的位置插入 80 节点。(底层插入完毕)
接下来用随机决定是否把这个 80 提升到上面的层中,例如图中的提升概率是 50%(抛硬币),不断提升至硬币为反面为止。
上面一段描述了 gif 中插入 80 的搜索和插入过程。那么,代码如何实现?右移和下移的逻辑很浅显,那么重点就在如何提升节点到上层的逻辑。
阅读更多…